
On the next lesson we will learn about differentiable functions. Again, the following useful tool is available: finding the equation of the tangent line to the graph of a function at a given point.
Tangent line how to#
🙂īy drawing the function and the tangent line we can see that our results are correct:Īs for this lesson about how to find the equation of the tangent line of a function at a given point we are done. Because the slopes of perpendicular lines (neither of. \Īnd this is the equation we were looking for. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency. Moving the term \( -y_0 \) to the right-hand side:Īnd since \( y_0 = f(x_0) \) we conclude: That is, performing multiplication on the right-hand side: So, once we have \( f'(x) \) we are able to evaluate \( f'(x_0) \), which is the slope \( m \). In other words, the derivative of a function on a point equals the slope of the tangent line to the function graph at that point. Given the geometrical meaning of the derivative of a function, we have: The equation of a line passing through the point \( (x_0, y_0) \) with slope \( m \) is: When both (i) and (ii) are satisfied, the vertical line x a is a tangent line of the curve y f(x) at the point (a, f(a)).

We will also have a look at a simple practical example.įinding the general form of the equation of the tangent line of a function graph knowing a point the line is passing through and its slope Here, the variable Cd lies on the x axis, so it is the independent variable. First, what is the equation of a line that passes through the origin, given that Cl and Cd are your variables.
Let’s now learn how to find the equation of the tangent line to a function graph at a given point. Then you want to find the point where a line that passes through the origin, is also tangent to the curve. Here on Altermath we also have a very useful tool: finding the equation of the tangent line to the function graph at a given point. Once we know the derivative function, we can get the slope of the tangent line by simply evaluating the derivative function itself at the point \( (x_0, y_0) \).Īnd now we have all that we need to write down the equation of the tangent line to the function graph at a given point \( (x_0, y_0) \).
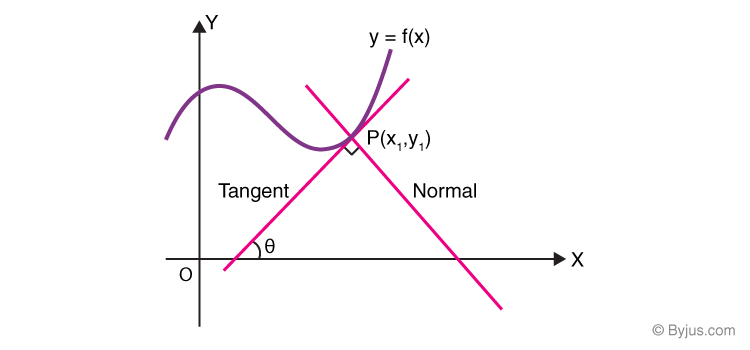
To do so, we just need the differentiation rules or, for those who don’t know them yet, the use of the derivative as seen as a limit of the difference quotient. But what is a tangent line The definition is trickier than you might think. A curve that is on the line passing through the points coordinates (a, f (a)) and has slope that is equal to f’ (a). Then, we will have to calculate the first derivative of the function. In calculus, youll often hear The derivative is the slope of the tangent line. That derivative actually represents the slope of the tangent line to the function graph at that very same point.Īs we will see, the key concept is the equation of the line having slope \( m \) and passing through the point \( (x_0, f(x_0)) \). Usually, that point will be the point where the tangent line touches the graph of. To find the complete equation, we need a point the line goes through. This lesson will demonstrate a practical use of the geometrical meaning of the derivative of a function at a given point. Choose 1 answer: Step 2 Evaluate the correct limit from the previous step. In the definition above, we state that our tangent line and curve will have the. The term “equation of the tangent line” refers to the expression of a function whose points \( (x, f(x)) \) all belong to the line being considered. the curve and tangent line have the same slope at the point ( x, y ). So let me see if I can, let me see if I can do this. So I could use that information to actually draw the tangent line. The slope of the tangent line, when x is equal to negative one is equal to negative two. In this lesson we will learn how to find the equation of the tangent line to a function graph at a given point. So the slope of the tangent line right at that point on our function is going to be negative two.


 0 kommentar(er)
0 kommentar(er)
